1.
(1)
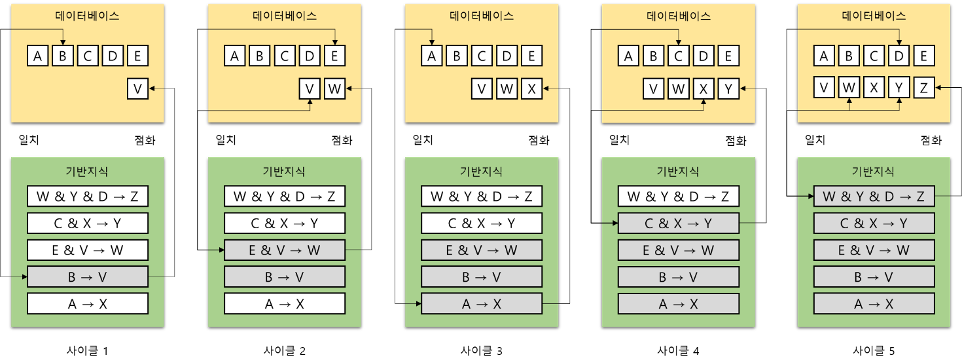
아래의 규칙들을 이용하여 전문가 시스템이 순방향 연결 추론으로 문제를 해결할 경우
초기 데이터베이스의 내용이 아래와 같이 주어질 때
문제의 해결과정에서 활성화되는 규칙과 점화되는 규칙, 데이터베이스의 내용을 단계별로 보이시오.
초기 데이터베이스 내용 : A B C D E
규칙 1 : W & Y & D → Z
규칙 2 : C & X → Y
규칙 3 : E & V → W
규칙 4 : B → V
규칙 5 : A → X
(2)
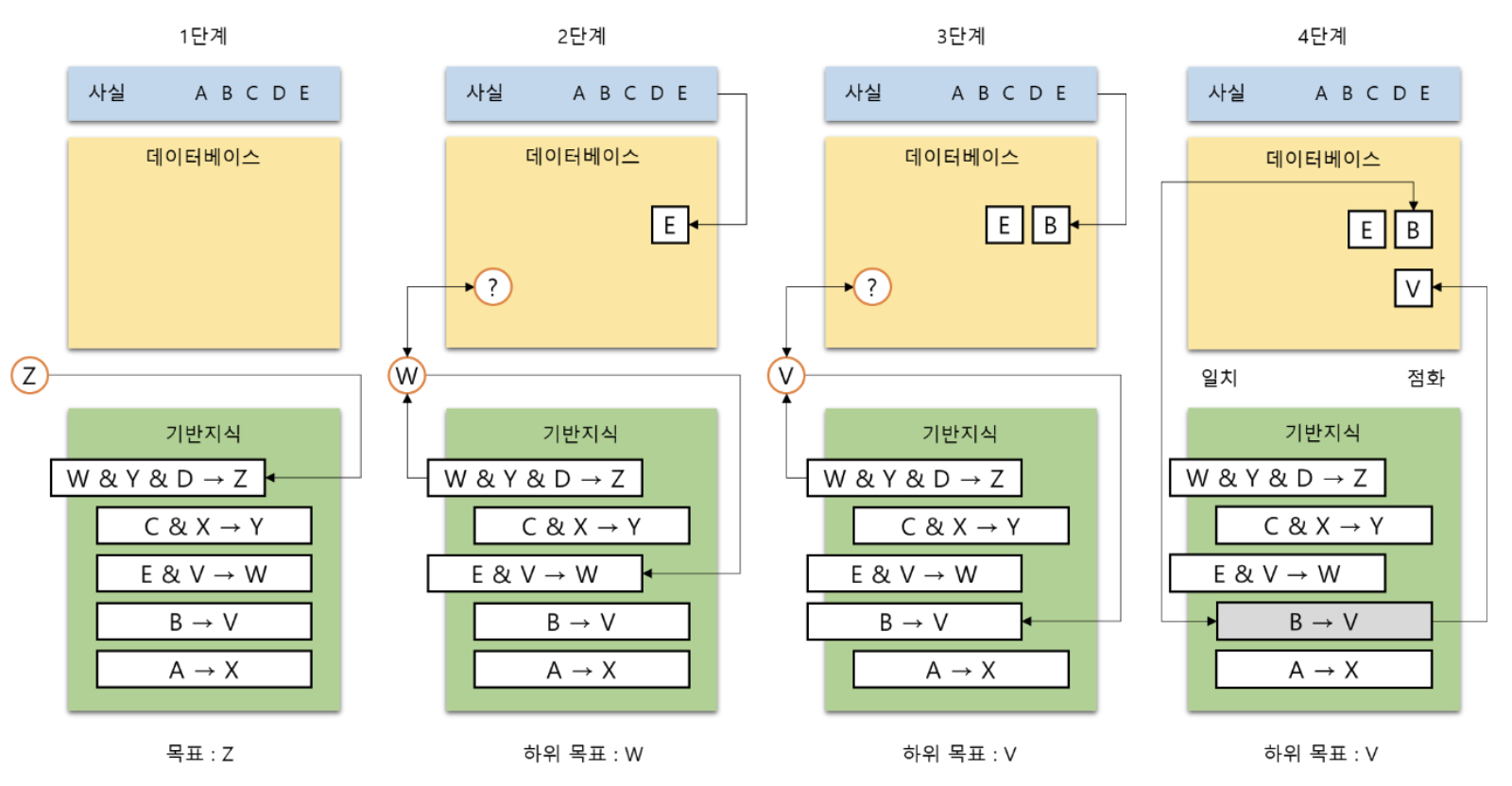
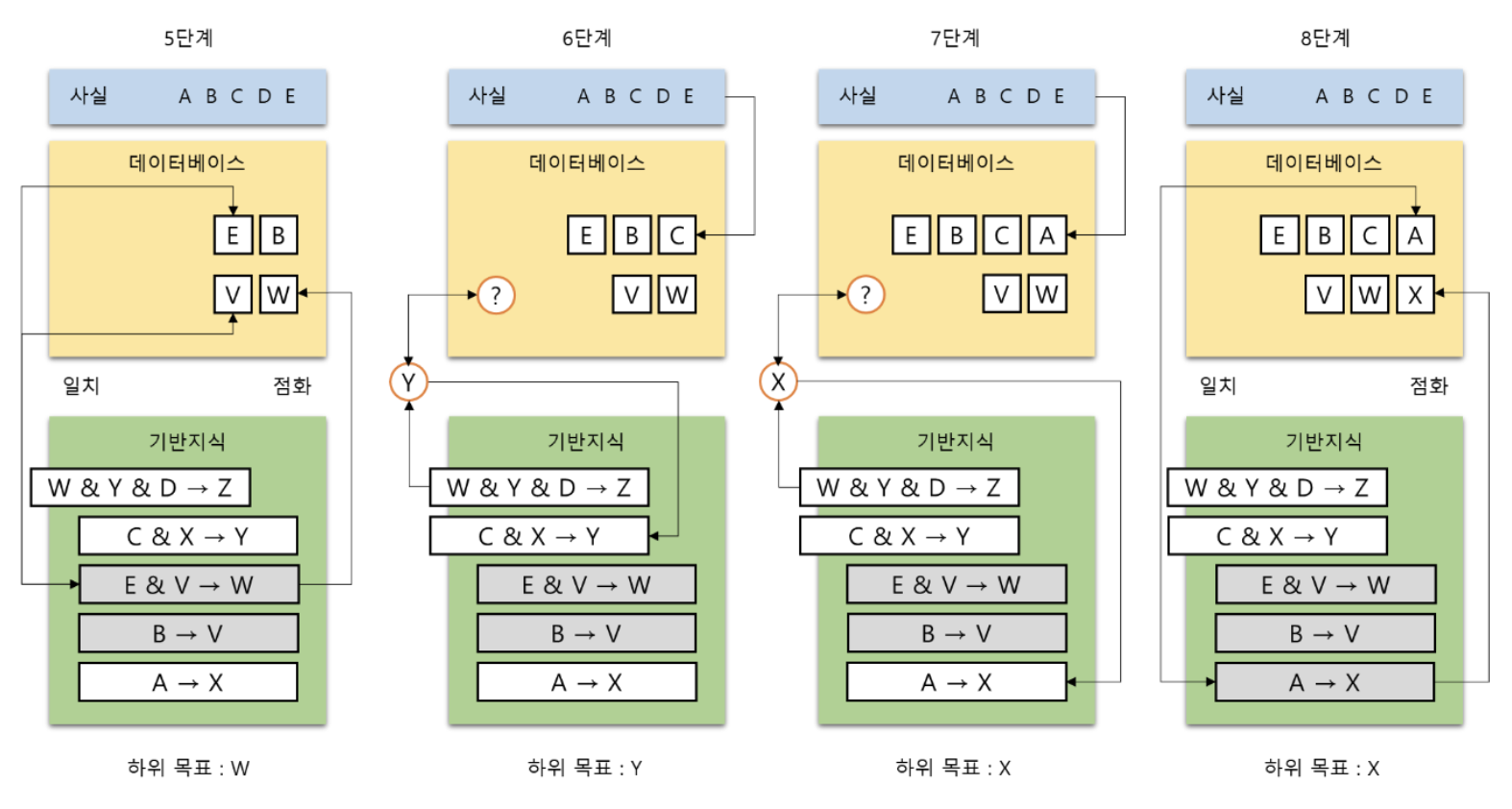
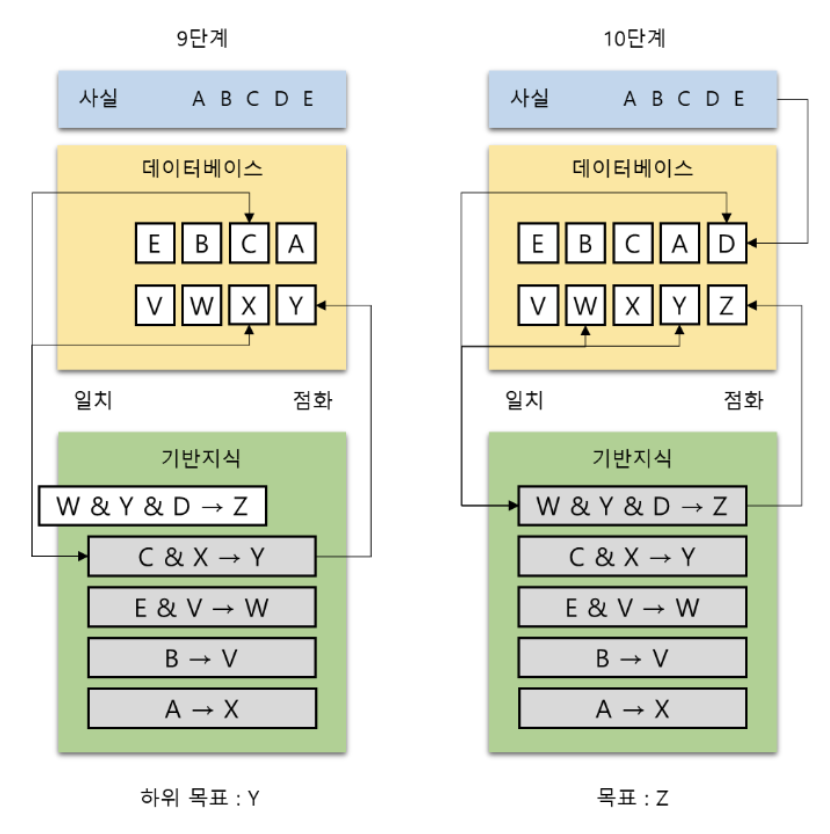
문제(1)에서 사실 Z에 대한 결론을 도출하기 위해 역방향 연결 추론을 사용할 때
추론 과정을 스택에 들어있는 규칙, 데이터베이스의 내용과 함께 단계별로 보이시오.
(추론 과정에서 A, B, C, D, E가 참으로 주어진다고 가정할 것)
2.
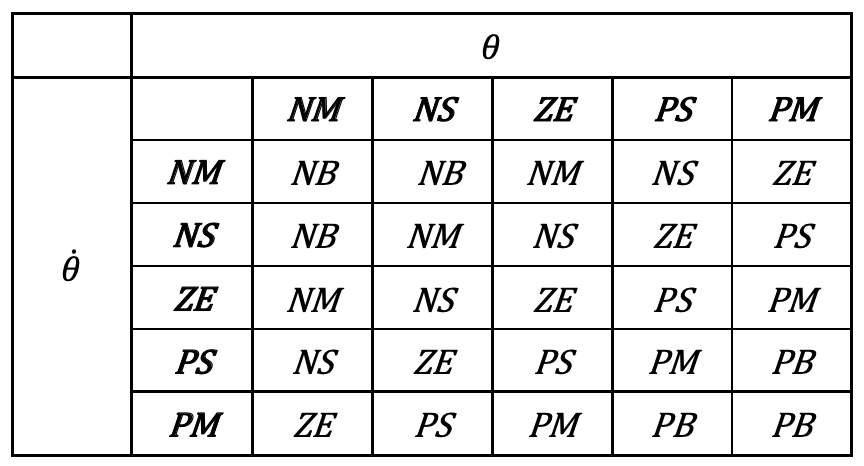
카트-역진자 제어 문제에 대해 다음 질문에 답하시오.
(문제 해결에 필요한 입력 𝜽, 𝜽̇과 출력 𝒇에 대한 소속함수와 퍼지 규칙은 강의 자료를 참고 할 것)
(1)
입력 𝜽=20, 𝜽̇ =15 에 대해 규칙을 평가한 결과와 이들을 결합한 결과를 그림으로 보이시오.
(평가 과정에서 클리핑을 사용하는 것으로 가정할 것)
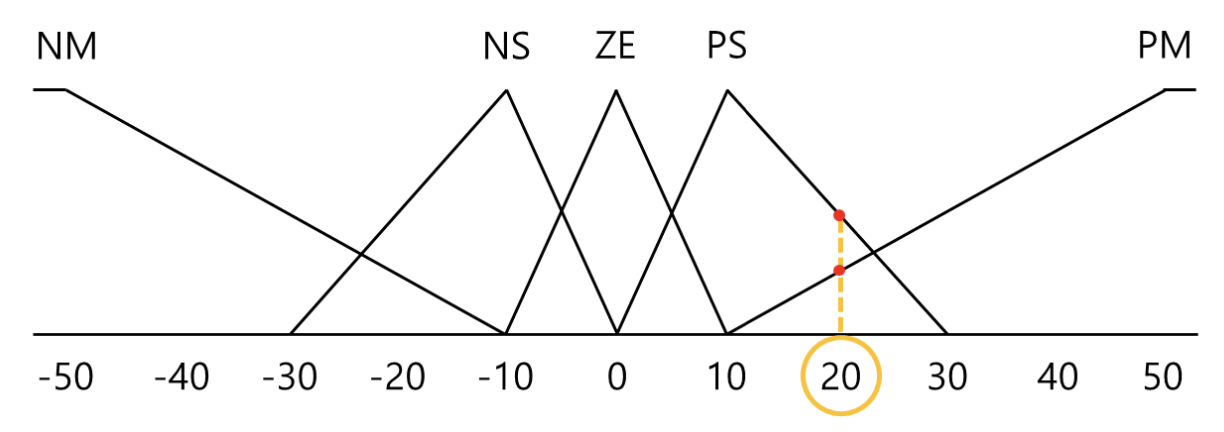
𝜽=20 일 때,
퍼지 집합 PS에 대한 소속 정도 ⇒ μ (𝜽) = 1/2 = 0.5
퍼지 집합 PM에 대한 소속 정도 ⇒ μ (𝜽) = 1/4 = 0.25
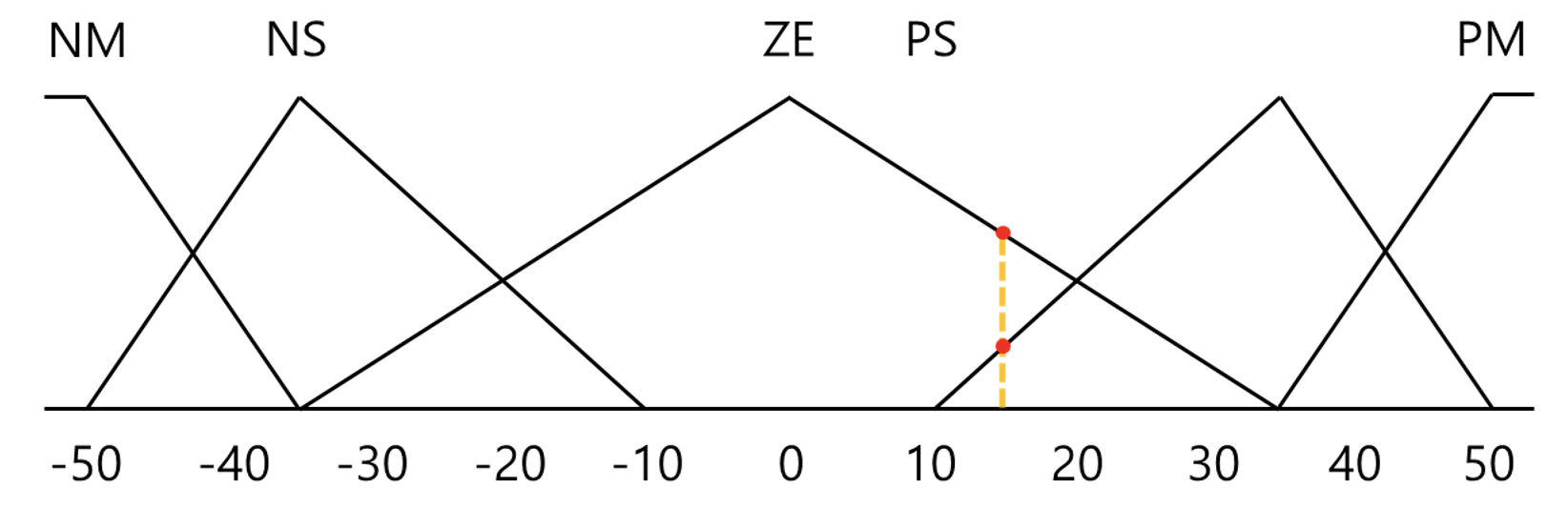
𝜽̇=15 일 때,
퍼지 집합 ZE에 대한 소속 정도 ⇒ μ (𝜽̇) = 4/7 = 0.57...
퍼지 집합 PS에 대한 소속 정도 ⇒ μ (𝜽̇) = 1/5 = 0.2
①
If 𝜃 =𝑷𝑺 AND 𝜃̇=𝒁𝑬, then 𝐹 = 𝑃𝑆
𝑷𝑺(𝜃 = 20) ∩ 𝒁𝑬(𝜃̇ = 15) = 𝑃𝑆(0.5)
②
If 𝜃 = 𝑷𝑺 AND 𝜃̇=𝑷𝑺, then 𝐹 = 𝑃𝑀
𝑷𝑺(𝜃 = 20) ∩ 𝑷𝑺(𝜃̇ = 15) = 𝑃𝑀(0.2)
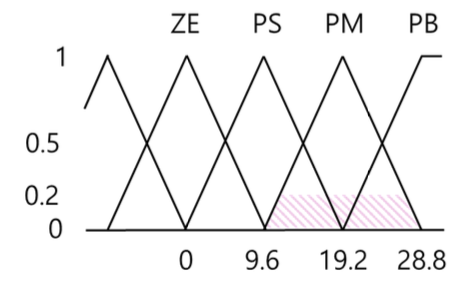
③
If 𝜃 = 𝑷𝑴 AND 𝜃̇=𝒁𝑬, then 𝐹 = 𝑃𝑀
𝑷𝑴(𝜃 = 20) ∩ 𝒁𝑬(𝜃̇ = 15) = 𝑃𝑀(0.25)
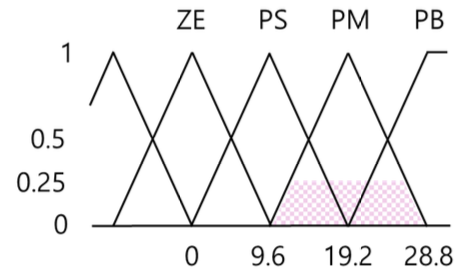
④
If 𝜃 = 𝑷𝑴 AND 𝜃̇=𝑷𝑺, then 𝐹 = 𝑃𝐵
𝑷𝑴(𝜃 = 20) ∩ 𝑷𝑺(𝜃̇ = 15) = 𝑃𝐵(0.2)
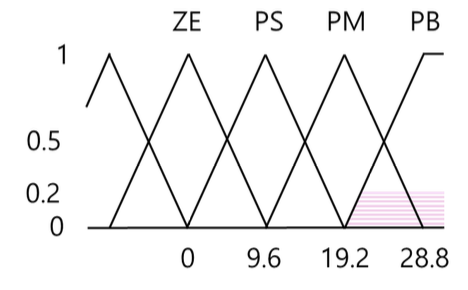
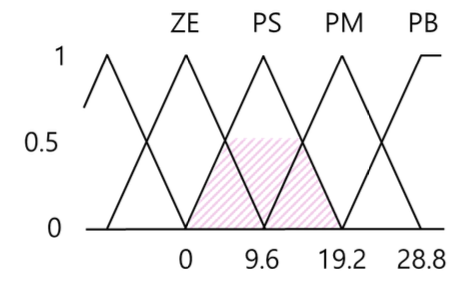
클리핑 처리된 모든 규칙의 후건들의 소속 함수를 퍼지 집합 하나로 결합하면,
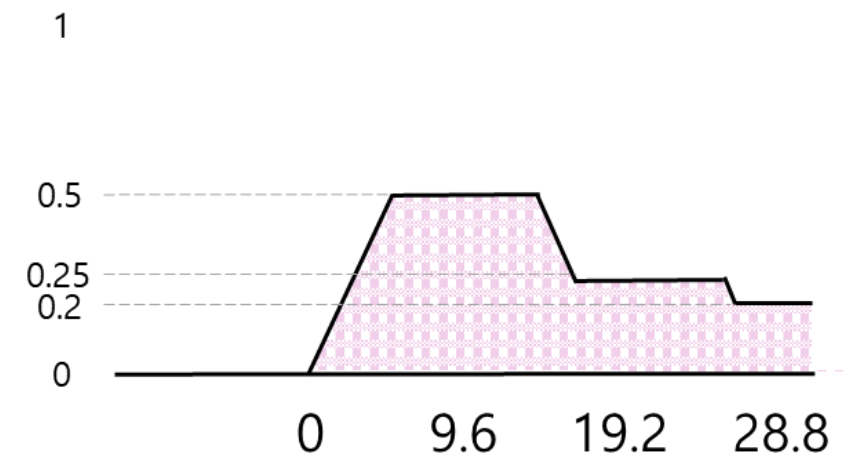
(2)
역퍼지화를 위한 방법으로 무게중심법을 사용하여 출력 𝒇을 구하시오.
(역퍼지화 과정에서는 힘 𝒇가 취하는 값이 0, 2.4, 4.8, 7.2, 9.6, ...의 이산 값으로 가정하고 출력 값을 계산할 것)
무게중심
= (2.4 + 16.8 + 19.2 + 21.6 + 24 + 26.4) * 0.25 + (4.8 + 7.2 + 9.6 + 12 + 14.4) * 0.5 + 28.8 * 0.2 / 0.25 * 6 + 0.5 * 5 + 0.2
= 57.36 / 4.2
= 13.657 ...
⚠️ 해당 무단 복제 및 전재, 재배포 금지 ⚠️
본 제작 자료 및 사진 이미지에 대한 저작권은 홈페이지 운영자 본인에게 있으며,
저작권에 위배되는 이미지 편집이나 무단 복제 및 무단 전재, 재배포 시 사전 경고 없이 형사 고발 조치됨을 알려드립니다.
